10-11 02:22 阅读 128

关注

概率论——常用分布

伯努利试验

　　伯努利试验（Bernoulli experiment）是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

　　我们假设该项试验独立重复地进行了 nn 次，那么就称这一系列重复独立的随机试验为 nn 重伯努利试验，或称为伯努利概型。单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的，多少是失败的，事情就变得有意义了，这些累计记录包含了很多潜在的非常有用的信息。

　　如果无穷随机变量序列  X1,X2,…X1,X2,…  是独立同分布 (i.i.d.)(i.i.d.) 的，而且每个随机变量  XiXi  都服从参数为  pp  的伯努利分布, 那么 随机变量  X1,X2,…X1,X2,…  就形成参数为  pp  的一系列伯努利试验。同样，如果 nn 个随机变量  X1,X2,…,XnX1,X2,…,Xn  独立同分布，并且都服从参数为 pp 的伯努利分布，则随机变量  X1,X2,…,XnX1,X2,…,Xn  形成参数为  pp  的 nn 重伯努利试验。

　　下面举几个例子加以说明，假定重复抛掷一枚均匀硬币，如果在第 ii 次抛掷中出现正面，令 Xi=1Xi=1 ；如果出现反面Xi=0Xi=0，那么，随机变量  X1,X2,…X1,X2,…  就形成参数为  p=12p=12  的一系列伯努利试验，同样，假定由一个特定机器生产的零件中  10%10%  是有缺陷的，随机抽取 nn 个进行观测，如果第 1 个零件有缺陷，令  Xi=1Xi=1 ;  如果没有缺陷，令  Xi=0,i=1,2,…,nXi=0,i=1,2,…,n ， 那么，随机变量  X1,X2,…,XnX1,X2,…,Xn 就形成参数为  p=110p=110  的 nn 重伯努利试验。

离散分布

二项分布

　　定义：在 nn 次独立重复的伯努利试验中，设每次试验中事件 AA 发生的概率为 pp。用 XX 表示 nn 重伯努利试验中事件 AA 发生的次数，则 XX 的可能取值为 0，1，…，n0，1，…，n ，且对每一个 kk（0≤k≤n0≤k≤n），事件 X=kX=k 即为 “ nn 次试验中事件 AA 恰好发生 kk 次”，随机变量 XX 的离散概率分布即为二项分布（Binomial Distribution）。

　　记  XX  为  nn  重伯努利试验中成功的事件 (记为  AA  ) 的次数，则  X=0,1,2,⋯,nX=0,1,2,⋯,n 。 XX  服从二项分布，记  pp  为事件  AA  发生的概率， XX  的分布列为：

　　　　P{X=k}=(nk)pk(1−p)n−k,k=0,1,⋯,nP{X=k}=(nk)pk(1−p)n−k,k=0,1,⋯,n

　　记做

　　　　X∼b(n,p)X∼b(n,p)

　　　　或：X∼B(n,p)X∼B(n,p)

 　　符号“~”读作“服从于”，该记号表示随机变量 XX 服从参数为 n,pn,p 的二项分布。

　　数学期望：npnp
　　方差：np(1−p)np(1−p)

　　举例：

　　1. 设射手命中率为 0.80.8 ，则射击 nn 次, 命中的次数 X∼b(n,0.8)X∼b(n,0.8) .
　　2. 已知人群中色盲率为 pp ， 在人群中随机调查50个人，则其中色盲患者 X∼b(50,p)X∼b(50,p) .
　　3. 某药品的有效率为 0.90.9 , 今有 1010 人服用，则服药有效的人数 X∼b(10,0.9)X∼b(10,0.9) .
　　4.......

两点分布

　　两点分布：是一种当 n=1n=1 时的特殊的二项分布，又名 0−10−1分布，伯努利分布，用来描述一次伯努利试验中成功的次数 XX，其中X=0,1X=0,1 。XX 服从两点分布， 分布列为:

　　　　P(X=x)=px(1−p)1−x,x=0,1P(X=x)=px(1−p)1−x,x=0,1

　　或表示为：

 　　　　XP01−p1pX01P1−pp

　　其中 p=P(X=1)p=P(X=1) 为事件成功的概率。
　　举例：
　　1. 小明投篮命中率为 0.80.8 ，投篮一次，其命中的次数 X∼b(1,0.8)X∼b(1,0.8) ；
　　2. 彩票中奖率为 0.00010.0001 , 小明购买一张彩票, 其中奖的次数 X∼b(1,0.0001)X∼b(1,0.0001)；
　　3. 不会做的单项选择题做对的概率为 0.250.25 ，随机选择一个选项, 做对的次数 X∼b(1,0.25)X∼b(1,0.25)；
　　4. …………
　　两点分布是特殊的二项分布， 在二项分布数学期望和方差的公式中取 n=1n=1 得到两点分布:

　　数学期望： pp
　　方差: p(1−p)p(1−p)

　　二项分布与两点分布的关系：若有一列独立同分布于 b(1,p)b(1,p) 的随机变量序列 {Xi}ni=1{Xi}i=1n , 则其和:

　　　　X1+X2+⋯+Xn=∑ni=1Xi∼b(n,p)X1+X2+⋯+Xn=∑i=1nXi∼b(n,p)

　　这个结论表明两点分布具有可加性，且对于服从 b(n,p)b(n,p) 的随机变量 XX ， 可看做由 nn 个独立 同分布于 b(1,p)b(1,p) 的随机变量 XiXi 的和。

泊松分布

　　Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。

　　泊松分布的概率函数为：

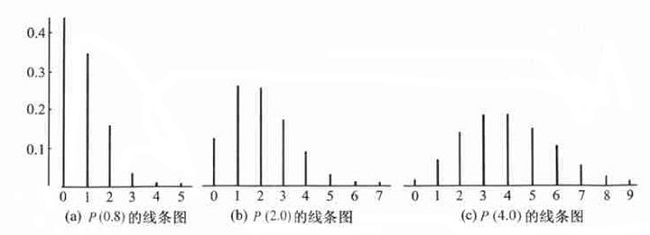
　　　　P(X=k)=λkk!e−λ,k=0,1,2,⋯P(X=k)=λkk!e−λ,k=0,1,2,⋯

　　泊松分布的参数 λλ 是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。

　　记 X∼P(λ)X∼P(λ)，常与单位时间、单位面积、单位体积上的计数过程相联系。

　　数学期望: λλ

　　方差: λλ

　　这里数学期望为 λλ 是指 XX 的均值为 λλ 。譬如对于应用举例 1，某段时间内，来到某商场的顾客数平均而言是  λλ 。其他的应用类似。

　　举例：

　　1. 某时间段内，来到某商场的顾客数；

　　2. 单位时间内，某网站的点击量；

　　3. 一平方米内玻璃上的气泡数；

　　4. …………

均匀分布

　　若随机变量 XX 的密度函数为：
　　　　p(x)={1b−a,0,a<x<b 其他. p(x)={1b−a,a<x<b0, 其他. 

　　称 XX 服从区间  (a,b)(a,b)  上的均匀分布，记作 X∼U(a,b)X∼U(a,b)，其分布函数:

　　　　F(x)=⎧⎩⎨⎪⎪0,x−ab−a,1,x<aa≤x<bx≥bF(x)={0,x<ax−ab−a,a≤x<b1,x≥b

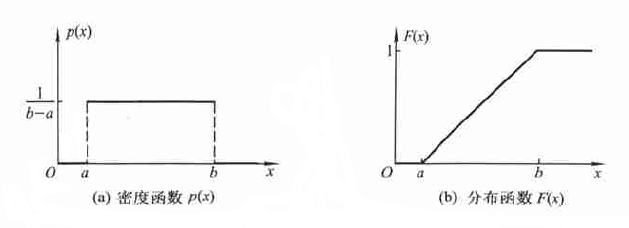
　　均匀分布又称作平顶分布（因其概率密度为常值函数）。

　　数学期望: a+b2a+b2
　　方差: (b−a)212(b−a)212

超几何分布

 　　有  NN  件产品，其中有  MM  件不合格品。若从中不放回地随机抽取  nn  件，则其中含有的不合格品的件数  XX  服从超几何分布，分布列为:

 　　　　P(X=k)=CkMCn−kN−MCnN=(Mk)(N−Mn−k)(Nn),k=0,1,⋯,rP(X=k)=CMkCN−Mn−kCNn=(Mk)(N−Mn−k)(Nn),k=0,1,⋯,r。

　　记为 X∼h(n,N,M)X∼h(n,N,M)。其中 r=min{M,n}r=min{M,n}，且 M⩽N,n⩽NM⩽N,n⩽N 。n,N,Mn,N,M 均为正整数。
　　举例：从有 10 件不合格品的 100 件产品中随机抽取 5 件，则抽取的产品中不合格品数   X∼h(5,100,10)X∼h(5,100,10)。

　　数学期望：n∙MNn∙MN

　　方差：D(X)=nMN(1−MN)N−nN−1D(X)=nMN(1−MN)N−nN−1

　　超几何分布和二项分布的联系

　　(1) 在超几何分布中，当 N→+∞N→+∞ 时， MN→PMN→P (二项分布中的 pp) 。
　　(2) 当 N→+∞N→+∞ 时，超几何分布的数学期望

　　　　EX=nMN→np=EXEX=nMN→np=EX

　　(3) 当 N→+∞N→+∞ 时，超几何分布的方差 DX=np(1−p)DX=np(1−p) (二项分布的方差) 。
　　(4) 当 N→+∞N→+∞ 时，超几何分布近似为二项分布。

几何分布

　　在伯努利试验序列中，记每次试验中事件 AA 发生的概率为 pp，如果 XX 为事件 AA 首次出现时的试验次数。详细地说，是：前 k−1k−1 次皆失败，第 kk 次成功的概率。则 X=1,2,⋯X=1,2,⋯ 。XX 服从几何分布，分布列为：
　　P(X=k)=(1−p)k−1p,k=1,2,⋯P(X=k)=(1−p)k−1p,k=1,2,⋯
　　记作 X∼Ge(p)X∼Ge(p) 。
　　举例:
　　1. 某产品的不合格率为 0.05 ， 首次查到不合格品的检查次数 X∼Ge(0.05)X∼Ge(0.05)
　　2. 某射手的命中率为 0.8 , 首次命中的射击次数 X∼Ge(0.8)X∼Ge(0.8)
　　3. 掷一颗骰子，首次出现六点的投郑次数 X∼Ge(16)X∼Ge(16)
　　4. .....

　　数学期望： 1p1p
　　方差: 1−pp21−pp2

　　几何分布的无记忆性：

　　设 X∼Ge(p)X∼Ge(p) ，对任意正整数 m,nm,n ，有:

　　　　P(X>m+n∣X>m)=P(X>n)P(X>m+n∣X>m)=P(X>n)

　　该性质表明，在前 mm 次试验中 AA 没有出现的条件下，则在接下去的 nn 次试验中 AA 仍末出现 的概率只与 nn 有关，而与以前的 mm 次试验无关，似乎忘记了前 mm 次试验结果， 这就是无记忆 性。

负二项分布

 　　在伯努利试验序列中，记每次试验中事件  AA 发生的概率为  pp  ，如果  XX  为事件  AA  第  rr  次出 现时的试验次数，则  XX  的可能取值为  r,r+1,⋯,r+m,⋯r,r+1,⋯,r+m,⋯ ，  称 XX 服从负二项分布或巴斯卡分布，其分布列为：

 　　P(X=k)=(k−1r−1)pr(1−p)k−r,k=r,r+1,⋯P(X=k)=(k−1r−1)pr(1−p)k−r,k=r,r+1,⋯

　　记作： X∼Nb(r,p)X∼Nb(r,p) , 当 r=1r=1 时即为几何分布，即几何分布是特殊的负二项分布。从二项分布和负二项分布的定义中看出，二项分布是伯努利试验次数 (nn) 固定，事件 AA 成功的次数 XX 在 0∼n0∼n 中取值；而负二项分布是事件 AA 成功的次数 ( rr ) 固定，伯努利实验次数 XX 在 r,r+1,⋯r,r+1,⋯ 中取值，可见负二项分布的 "负" 字的由来。

数学期望： rprp
方差: r(1−p)p2r(1−p)p2

　　从负二项分布和几何分布的数学期望和方差的关系可知，类比二项分布与两点分布的关系，可以得 到下面的结论：
　　若有一列独立同分布于 Ge(p)Ge(p) 的随机变量序列 {Xi}ni=1{Xi}i=1n , 则其和：

　　　　X1+X2+⋯+Xr=∑i=1rXi∼Nb(r,p)X1+X2+⋯+Xr=∑i=1rXi∼Nb(r,p)

　　这并不是说明几何分布具有可加性，因为可加性要求服从该类分布的随机变量的和仍服从该类分布，但是服从几何分布的随机变量的和服从负二项分布，这个概念要特别注意。上述结论只能说明 对于服从 Nb(r,p)Nb(r,p) 的随机变量 XX ，可看做由 rr 个独立同分布于 Ge(p)Ge(p) 的随机变量 XiXi 的和。

常用连续分布

正态分布

　　正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。

　　若随机变量 XX 的密度函数为:

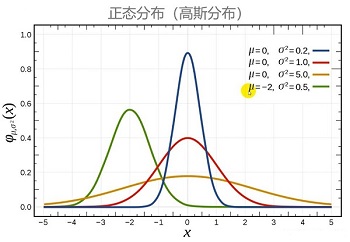
　　　　p(x)=12π√σe−(x−μ)22σ2,−∞<x<∞p(x)=12πσe−(x−μ)22σ2,−∞<x<∞

　　则称 XX 服从正态分布，称 XX 为正态变量。记 X∼N(μ,σ2)X∼N(μ,σ2)。其中 μμ 为位置参数，用于控制曲线在 xx 轴上的位置； σσ 为尺度参数，用于控制曲线的形状。

　　正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
　　分布函数：

　　　　F(x)=∫x−∞p(t)dt=∫x−∞12π√σe−(t−μ)22σ2 dtF(x)=∫−∞xp(t)dt=∫−∞x12πσe−(t−μ)22σ2 dt

数学期望：μμ

方差: σ2σ2

　　称 μ=0,σ2=1μ=0,σ2=1 时的正态分布为标准正态分布，其密度函数和分布函数分别为:

　　　　φ(x)=12π√e−x22Φ(x)=∫x−∞φ(t)dt=∫x−∞12π√e−t22 dtφ(x)=12πe−x22Φ(x)=∫−∞xφ(t)dt=∫−∞x12πe−t22 dt

　　任何一个正态变量均可以通过标准化转化为标准正态变量，即若 X∼N(μ,σ2)X∼N(μ,σ2)，则:

　　　　X∗=X−μσ∼N(0,1)X∗=X−μσ∼N(0,1)

　　其中 X∗X∗ 为标准正志变量。

　　性质：

　　若 X∼N(0,1)X∼N(0,1) : 　　　　

　　　　Φ(−a)=1−Φ(a)P(X>a)=1−Φ(a)P(a<x<b)=Φ(b)−Φ(a)P(|X|<c)=2Φ(c)−1,(c≥0)Φ(−a)=1−Φ(a)P(X>a)=1−Φ(a)P(a<x<b)=Φ(b)−Φ(a)P(|X|<c)=2Φ(c)−1,(c≥0) 　　

　　若 X∼N(μ,σ2)X∼N(μ,σ2)： 　　　　

　　　　P(X≤c)=Φ(a−μσ)P(a<x≤b)=Φ(b−μσ)−Φ(a−μσ)P(X≤c)=Φ(a−μσ)P(a<x≤b)=Φ(b−μσ)−Φ(a−μσ) 　　

　　正态分布的 3σ3σ 原则： 　　　　

　　　　P(|X−μ|<kσ)=Φ(k)−Φ(−k)=2Φ(k)−1=⎧⎩⎨⎪⎪0.6826,0.9545,0.9973,k=1k=2k=3P(|X−μ|<kσ)=Φ(k)−Φ(−k)=2Φ(k)−1={0.6826,k=10.9545,k=20.9973,k=3

均匀分布

　　若随机变量 XX 的密度函数为:

　　　　p(x)={1b−a,0,a<x<b 其他. p(x)={1b−a,a<x<b0, 其他. 

　　称 XX 服从区间 (a,b)(a,b) 上的均匀分布，记作 X∼U(a,b)X∼U(a,b) , 其分布函数:

　　　　F(x)=⎧⎩⎨⎪⎪0,x−ab−a,1,x<aa≤x<bx≥bF(x)={0,x<ax−ab−a,a≤x<b1,x≥b

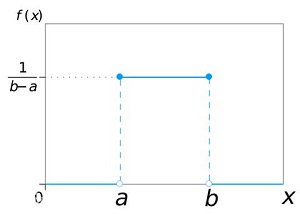
　　均匀分布又称作平顶分布（因其概率密度为常值函数）。

　　数学期望： a+b2a+b2
　　方差：(b−a)212(b−a)212

指数分布

　　若随机变量 XX 的密度函数为：

　　　　p(x)={λe−λx,0,x≥0x<0p(x)={λe−λx,x≥00,x<0

　　则称 XX 服从参数为 λλ 的指数分布，记作 X∼Exp(λ)X∼Exp⁡(λ) 。指数分布的分布函数为:

　　　　F(x)={1−eλx,0,x≥0x<0F(x)={1−eλx,x≥00,x<0

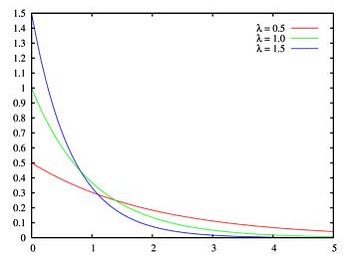
　　指数分布是一种偏态分布，指数分布随机变量只可能取非负实数。指数分布常被用作各种“寿命”分布，譬如电子元器件的寿命、动物的寿命、电话的通话时间、随机服务系统中的服务时间等都可假定服从指数分布。指数分布在可靠性与排队论中有着广泛的应用.。

　　数学期望: 1λ1λ
　　方差: 1λ21λ2

　　指数分布的无记忆性
　　若随机变量 X∼Exp(λ)X∼Exp⁡(λ) ， 则对任意的 t>0,s>0t>0,s>0 ， 有:
　　　　P(X>s+t∣X>s)=P(X>t)P(X>s+t∣X>s)=P(X>t)
　　证明:
　　因为 X∼Exp(λ)X∼Exp⁡(λ) ， 所以 P(X≥s)=e−λs,(s>0)P(X≥s)=e−λs,(s>0)。又因为
　　　　{X>s+t}⊆{X>s}{X>s+t}⊆{X>s}
　　由条件概率可得：

　　　　P(X>s+t∣X>s)=P(X>s+t)P(X>s)=e−λ(s+t)e−λt=e−λt=P(X>t)P(X>s+t∣X>s)=P(X>s+t)P(X>s)=e−λ(s+t)e−λt=e−λt=P(X>t)

　　证毕。

伽玛分布

　　若随机变量 XX 的密度函数为：

　　　　p(x)={λaΓ(α)xa−1e−λx,0,x⩾0x<0p(x)={λaΓ(α)xa−1e−λx,x⩾00,x<0

　　称 XX 服从伽玛分布, 记作 X∼Ga(α,λ)X∼Ga(α,λ) 。其中 α>0α>0 为形状参数，λ>0λ>0 为尺度参数。

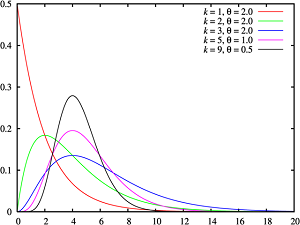
　　数学期望: αλαλ

　　方差: αλ2αλ2
　　伽玛函数的特例：
　　1. α=1α=1 时的伽玛分布为指数分布: Ga(1,λ)=Exp(λ)Ga(1,λ)=Exp⁡(λ) ,
　　2.称 α=n2α=n2, λ=12λ=12 的伽玛分布为自由度为 nn 的 χ2χ2 (卡方) 分布，记作 χ2(n)χ2(n) :

　　　　Ga(n2,12)=χ2(n)Ga(n2,12)=χ2(n)

　　因卡方分布是特殊的伽玛分布，故不难求得卡方分布的：

　　数学期望： nn　　

　　方差： 2n2n

　　卡方分布的唯一参数 nn 称为它的自由度, 具体含义在之后的数理统计中会给出。

贝塔分布

　　先给出贝塔函数：

　　　　B(a,b)=∫10xa−1(1−x)b−1dxB(a,b)=∫01xa−1(1−x)b−1dx
　　其中参数 a>0,b>0a>0,b>0 。贝塔函数具有以下性质：
　　1. B(a,b)=B(b,a)B(a,b)=B(b,a)
　　2.贝塔函数与伽玛函数有如下关系：
　　　　B(a,b)=Γ(a)Γ(b)Γ(a+b)B(a,b)=Γ(a)Γ(b)Γ(a+b)
　　贝塔分布:
　　若随机变量 XX 的密度函数为：

　　　　p(x)={Γ(a)Γ(b)Γ(a+b)xa−1(1−x)b−1,0,0<x<1 其他. p(x)={Γ(a)Γ(b)Γ(a+b)xa−1(1−x)b−1,0<x<10, 其他. 

　　则称 XX  服从贝塔分布, 记作 X∼Be(a,b)X∼Be(a,b) , 其中 a>0,b>0a>0,b>0  都是形状奈数。

数学期望: a(a+1)(a+b)(a+b+1)a(a+1)(a+b)(a+b+1)
方差: ab(a+b)2(a+b+1)